This document is one of More SageMath Tutorials. You may edit it on github. \(\def\NN{\mathbb{N}}\) \(\def\ZZ{\mathbb{Z}}\) \(\def\QQ{\mathbb{Q}}\) \(\def\RR{\mathbb{R}}\) \(\def\CC{\mathbb{C}}\)

Option Algèbre et Calcul Formel de l’Agrégation de Mathématiques: Algèbre linéaire rapide¶

Dans ce cours, nous explorons quelques limites de l’algorithme de Gauß en terme de performances, et donnons des approches pour les contourner.

Todo

ajouter des #random où utile; mettre les %display latex juste là où c’est utile

Todo

ajouter des exercices pour les faire manipuler

Méthodes modulaires et généralisations¶

Introduction¶

On a vu que l’algorithme de Gauß était de complexité \(O(n^3)\), au moins dans son implantation naïve. Vérifions cela expérimentalement avec les petits outils du fichier gauss.py:

sage: %runfile media/gauss.py

sage: m = matrice_inversible(3, GF(7)); m   # random
[1 0 0]
[0 6 2]
[2 5 0]

sage: gauss(m)                              # random
[3 1 6]
[0 2 6]
[0 0 2]

Commençons par un corps fini:

sage: import functools
sage: construit_donnee = functools.partial(matrice_inversible, corps=GF(7))

sage: construit_donnee(3)                   # random
[5 4 5]
[6 2 2]
[1 2 5]

sage: temps(gauss, 10, construit_donnee)    # random
0.00010991096496582031
sage: temps(gauss, 20, construit_donnee)    # random
0.0004279613494873047

sage: t = [temps(gauss, 2^k, construit_donnee) for k in range(9)]; t     # random
[1.2874603271484375e-05,
 2.193450927734375e-05,
 3.0994415283203125e-05,
 7.295608520507812e-05,
 0.00026416778564453125,
 0.0012059211730957031,
 0.007287025451660156,
 0.04861617088317871,
 0.3510730266571045]
sage: [ t[i+1]/t[i] for i in range(len(t)-1) ]    # random
[1.7037037037037037,
 1.4130434782608696,
 2.353846153846154,
 3.6209150326797386,
 4.564981949458484,
 6.04270462633452,
 6.671607119486978,
 7.221322047363801]

Un peu plus de valeurs supplémentaires calculées au préalable:

sage: t = [2.8848648071289062e-05, 2.9087066650390625e-05, 4.1961669921875e-05, 9.298324584960938e-05, 0.0003731250762939453, 0.0017020702362060547, 0.010125160217285156, 0.04890704154968262, 0.3750150203704834, 2.7238361835479736, 20.545907974243164, 182.26634407043457, 1334.3144991397858]

sage: [ t[i+1]/t[i] for i in range(len(t)-1) ]
[1.0082644628099173, 1.4426229508196722, 2.215909090909091, 4.012820512820513, 4.561661341853035, 5.948732315450343, 4.830248657812941, 7.667914649662898, 7.263272230688392, 7.543004274023845, 8.871174946316705, 7.320685044432319]
sage: points(enumerate(_))

C’est plausible.

Prenons maintenant le corps des rationnels:

sage: construit_donnee = functools.partial(matrice_inversible, corps=QQ)
sage: t = [temps(gauss, 2^k, construit_donnee) for k in range(8)]; t   # random
[2.7179718017578125e-05, 3.910064697265625e-05, 0.00010395050048828125, 0.0005209445953369141, 0.003559112548828125, 0.028071880340576172, 0.25052881240844727, 2.8525619506835938]

sage: t = [6.389617919921875e-05, 0.00010395050048828125, 0.000308990478515625, 0.001764059066772461, 0.012479066848754883, 0.09727597236633301, 0.8789999485015869, 9.599533081054688, 127.58634281158447, 2059.1530270576477]
sage: [ t[i+1]/t[i] for i in range(len(t)-1) ]
[1.62686567164179, 2.97247706422018, 5.70910493827161, 7.07406406271118, 7.79513192334881, 9.03614661585030, 10.9209711529777, 13.2908904770988, 16.13929031650778]

Bof …

Avec la matrice de Hilbert:

sage: def hilbert(n):
....:     return matrix(QQ, n, n, lambda i,j: 1/(1+i+j))
....: hilbert(3)
[  1 1/2 1/3]
[1/2 1/3 1/4]
[1/3 1/4 1/5]

sage: [temps(gauss, 2^k, hilbert) for k in range(8)]              # random
[9.393692016601562e-05, 4.887580871582031e-05, 0.000102996826171875, 0.0005269050598144531, 0.003654003143310547, 0.028528928756713867, 0.23932909965515137, 2.2389848232269287]
sage: t = [2.193450927734375e-05, 3.4809112548828125e-05, 9.202957153320312e-05, 0.0004980564117431641, 0.003587961196899414, 0.029154062271118164, 0.2275228500366211, 2.2509679794311523, 25.5708429813385, 328.3195171356201]

sage: [ t[i+1]/t[i] for i in range(len(t)-1) ]
[1.58695652173913, 2.64383561643836, 5.41191709844560, 7.20392532312111, 8.12552329058409, 7.80415600134117, 9.89337105731950, 11.3599319115150, 12.8396047551200]

Bof!

Todo

Ces bancs d’essais suggèrent que la complexité n’est pas pire que \(O(n^4)\), ce qui n’est guère mieux que ce que l’on obtient en modulaire ou multimodulaire. Trouver quelque chose de plus frappant.

Prenons un corps de fractions rationnelles:

sage: K = QQ['x'].fraction_field()
sage: construit_donnee = functools.partial(random_matrix, K)

sage: construit_donnee(2)
[ (-3/8*x + 3/25)/(-1/13*x^2 + 1/3*x)                       (-1/3*x - 1)/(-2*x^2 + x + 1)]
[ (4/169*x^2 + 1/9*x)/(x^2 + 9*x - 1/5)  (-1/2*x^2 + 1/2*x + 207)/(2/7*x^2 + 3/2*x + 1/2)]

sage: t = [temps(gauss, n, construit_donnee) for n in range(10)]; t
[1.3113021850585938e-05, 2.193450927734375e-05, 0.00019097328186035156, 0.0006430149078369141, 0.0026559829711914062, 0.0067059993743896484, 0.01826310157775879, 0.04449200630187988, 0.11454296112060547, 0.6179559230804443]

sage: t = [1.1920928955078125e-05, 1.9073486328125e-05, 0.00018310546875, 0.0007388591766357422, 0.002237081527709961, 0.007543087005615234, 0.021083831787109375, 0.08204507827758789, 0.15540504455566406, 0.9841179847717285, 22.702343940734863]
sage: [ t[i+1]/t[i] for i in range(len(t)-1) ]
[1.60000000000000, 9.60000000000000, 4.03515625000000, 3.02775088738303, 3.37184269423425,
2.79511979265440, 3.89137416319884, 1.89414219375687, 6.33259999754532, 23.0687217305563]

Analyse: Complexité arithmétique versus complexité en bits¶

Pourquoi est-ce que notre analyse de complexité est si éloignée de la réalité?

Parce que l’on a un mauvais modèle!

On a mesuré la complexité arithmétique de l’algorithme de Gauß, la métrique étant donnée par le nombre d’opérations arithmétiques.

Or, comme l’a constaté toute personne ayant calculé un pivot de Gauß à la main, les coefficients ont tendance à grossir:

sage: %display latex                                              # not tested
sage: gauss(matrice_inversible(10))                               # random
[       1        0       -2     -1/2        1        2        1        0       -1       -1]
[       0        1        0     -5/2        5        0        3        2        0       -3]
[       0        0        1     -5/4     11/2       -1        2      3/2      3/2     -5/2]
[       0        0        0        1    -14/9      8/9    -10/9     -2/3     -2/9      2/3]
[       0        0        0        0        1   -19/31   -11/62    -3/62    -2/31   -21/31]
[       0        0        0        0        0        1      5/6     -5/9     2/81    38/27]
[       0        0        0        0        0        0        1    -13/3   -74/27      7/9]
[       0        0        0        0        0        0        0        1  194/495  -94/165]
[       0        0        0        0        0        0        0        0        1 1467/436]
[       0        0        0        0        0        0        0        0        0        1]


sage: def max_coeff(m):
....:     return max([c.numer() for row in m.rows() for c in row])

sage: t = [ max_coeff(gauss(matrice_inversible(2^k))) for k in range(7) ] # random
sage: t
[1, 1, 1, 19, 4238342698, 99340450694580511972871852, 49519664469784658153819267407199333624664412533859761535203139]

Considérer que le temps nécessaire à une opération arithmétique est constant est donc abusif!

Une meilleure mesure est donc la complexité en bits, puisque les opérations arithmétiques sont de complexité polynomiale en \(n\) (en fait en gros \(n\log n\)) où \(n\) est le nombre de bits:

sage: tt = [x.ndigits(2) for x in t]
sage: [float(tt[i+1]/tt[i]) for i in range(len(t)-1)]
[1.0, 1.0, 2.0, 5.0, 2.6, 2.3846153846153846]

Cela suggère expérimentalement que, pour les rationnels, le nombre de bits est borné par un petit polynôme en \(n\).

Méthodes modulaires et multimodulaires¶

Todo

Donner les complexités explicites, quitte à ne pas les démontrer

Exemple: le calcul du déterminant¶

Exemple

Entrée: une matrice \(M\) à coefficients entiers

Sortie: son déterminant

C’est un problème typique: on a un résultat qui est relativement petit (un nombre) mais son calcul direct nécessite de manipuler pleins de gros coefficients.

Algorithme modulaire

Déterminer une borne \(b\) sur le déterminant (par ex: borne de Hadamard)
Choisir un grand nombre premier \(p>2b\)
Calculer \(\det(M)\) modulo \(p\):

\[\begin{split}\require{AMScd} \begin{CD} M @>{\ \det\ }>> \det(M)\\ @VV{\mod p}V @VV{\mod p}V \\ M\!\mod p @>{\ \det\ }>> \det(M\!\mod p) \end{CD}\end{split}\]

En déduire \(\det(M)\).

Algorithme multimodulaire

Comme ci-dessus
Choisir plusieurs (combien?) petits nombres premiers tels que \(p_1\cdots p_k>2b\)
Calculer \(\det(M)\) modulo \(p_i\) pour chaque \(i\)
Utiliser le lemme chinois pour reconstruire \(\det(M)\).

Intérêt du multimodulaire?

Calculer avec des corps finis dont les éléments tiennent dans un entier machine. Chaque opération arithmétique sur \(GF(p_i)\) correspond à un petit nombre d’opérations du processeurs.
Voire dans un flottant machine (seul intérêt: les processeurs actuels sont plus optimisés pour manipuler des flottants …).
Parallélisation

Exemple: bornes sur le rang¶

Remarque

\[\operatorname{rang} (M\mod p) \leq \operatorname{rang}(M)\]

Généralisations¶

La clef des algorithmes précédents est que l’on avait un morphisme du corps de base dans un/plusieurs corps où l’arithmétique était plus efficace, avec la possibilité d’inverser localement ce morphisme à la fin.

La même technique s’adapte à chaque fois que l’on a une explosion des coefficients intermédiaires, et un morphisme dans un (ou plusieurs) corps où l’on maîtrise la croissance des coefficients intermédiaires.

Exemple de problème

Entrée: une matrice \(M\) à coefficients polynomiaux

Sortie: son déterminant

Algorithme

Déterminer une borne \(k\) sur le degré du déterminant.
Choisir \(k\) éléments du corps de base.
Prendre le morphisme d’évaluation en ces points:

\[\begin{split}\phi: \begin{cases} K[x] & \rightarrow K^k\\ P & \mapsto (P(a_1), \dots, P(a_k)) \end{cases}\end{split}\]

Calculer \(\phi(\det(M))\) en se ramenant au calcul de \(k\) déterminants de matrices à coefficients dans le corps de base.
Reconstruire \(\det(M)\), par exemple par interpolation de Lagrange, FFT inverse, …

Exercice

Donner une borne de complexité pour le calcul du polynôme caractéristique d’une matrice dans \(GF(p)\).

Variante: méthodes \(p\)-adiques¶

Exemple de problème

Entrée: une matrice \(M\) carrée inversible à coefficients rationnels

Sortie: l’inverse de \(M\)

Que se passe-t’il si on prend \(M\) modulo \(p\)? modulo \(p^k\)

Expansion \(p\)-adique¶

Exercice: Expansion \(3\)-adique d’entiers

Voici quelques expansions \(3\)-adiques d’entiers:

sage: K = Zp(3)
sage: %display latex

sage: K(1)
1 + O(3^20)
sage: K(3)
3 + O(3^21)
sage: K(3^2)
3^2 + O(3^22)
sage: K(3^3)
3^3 + O(3^23)
sage: K(24)
2*3 + 2*3^2 + O(3^21)
sage: K(25)
1 + 2*3 + 2*3^2 + O(3^20)

Calculer l’expansion \(3\)-adique de \(15\) et de \(-1\).
Calculer le produit de \(1+2\cdot3 +2\cdot3^2+\cdots\) par \(4\).

Solutions

sage: K(15)
2*3 + 3^2 + O(3^21)
sage: K(-1)
2 + 2*3 + 2*3^2 + 2*3^3 + 2*3^4 + 2*3^5 + 2*3^6 + 2*3^7 + 2*3^8 + 2*3^9 + 2*3^10 + 2*3^11 + 2*3^12 + 2*3^13 + 2*3^14 + 2*3^15 + 2*3^16 + 2*3^17 + 2*3^18 + 2*3^19 + O(3^20)

sage: 1 / K(4)
1 + 2*3 + 2*3^3 + 2*3^5 + 2*3^7 + 2*3^9 + 2*3^11 + 2*3^13 + 2*3^15 + 2*3^17 + 2*3^19 + O(3^20)
sage: 1 / K(4) * K(4)
1 + O(3^20)

Tronquer revient à considèrer le morphisme partiel \(\phi\) de \(\QQ\) dans \(\ZZ/p^k\ZZ\):

Ce morphisme n’est définit que pour les rationnels \(x\) dont le dénominateur n’est pas divisible par \(p\)
Si on connaît \(\phi(x)\) pour \(k\) suffisamment grand, on peut retrouver \(x\) par reconstruction rationnelle. Rappel: encore une conséquence d’Euclide étendu!

Algorithme

Prendre un nombre premier \(p\) qui ne divise pas le déterminant de \(M\).
Une bonne stratégie est de choisir \(p\) au hasard! Statistiquement il sera bon, et sinon on s’en rendra compte et on recommencera.
Calculer l’inverse \(N\) de \(M\) modulo \(p\).
Raffiner itérativement cette solution: - Supposons que l’on ait \(N\) tel que \(MN=1\) modulo \(p^k\) - Prendre \(R\) tel que \(MN = 1+p^k R\) - Poser \(N':=N(1-p^kR)\) - Alors \(MN'=1-p^{2k} R\)
\(k\) double à chaque itération!!!
Lorsque \(k\) est suffisamment grand, on retrouve \(M^{-1}\) par reconstruction rationnelle de chacun de ses coefficients.

Mise en contexte: on a écrit notre matrice \(M\) comme une série:

\[M = M_0 + M_1 p + M_2 p^2 + \cdots\]

où chaque \(M_i\) est essentiellement une matrice mod \(p\), et on a utilisé la technique classique de l’itération de Newton pour calculer une solution de plus en plus précise de l’équation \(MN=1\).

Algorithmes de type «Boîte noire»¶

Problème¶

Considérons une matrice creuse:

sage: M = random_matrix(GF(7), 19, sparse=True, density=1/3)
sage: M
[2 0 0 0 2 2 0 2 0 0 0 4 0 0 3 5 0 0 0]
[2 0 0 0 0 3 0 6 0 0 3 0 6 0 3 5 6 0 5]
[3 6 2 0 2 2 0 3 2 1 1 0 1 6 6 0 0 1 0]
[0 4 6 2 0 1 0 0 0 6 0 5 0 0 2 2 2 1 0]
[0 0 0 6 2 0 0 1 0 5 2 0 0 0 0 0 4 1 0]
[0 0 4 0 0 0 0 0 0 4 0 0 0 2 0 0 2 0 0]
[0 0 0 0 2 0 0 2 0 0 3 5 0 4 0 1 0 0 0]
[6 0 0 0 0 6 0 0 0 4 5 0 0 3 6 4 0 0 4]
[0 0 0 0 0 0 2 0 0 1 4 0 0 0 6 0 0 2 0]
[0 1 4 0 0 6 5 0 5 0 6 3 3 0 0 0 0 0 2]
[2 0 0 2 0 2 0 0 0 0 0 4 0 6 0 0 4 0 0]
[4 0 1 0 4 0 0 0 0 0 3 5 0 0 3 0 0 2 0]
[0 4 0 6 0 0 0 0 5 6 0 0 1 5 5 4 0 5 3]
[0 0 5 0 6 0 2 2 5 5 2 1 3 0 0 4 0 0 5]
[0 0 5 0 5 0 0 4 0 0 0 0 5 4 0 2 0 0 0]
[0 0 0 0 0 0 0 4 0 0 0 0 0 5 0 0 0 0 3]
[0 1 3 4 0 1 0 0 0 4 0 0 0 0 0 1 5 6 0]
[6 0 5 0 0 0 0 0 0 0 1 0 6 0 0 0 0 0 0]
[5 0 0 2 0 0 6 6 0 6 0 5 0 0 0 0 0 0 0]

Et appliquons un pivot de Gauß partiel:

sage: gauss(M,10)
[1 0 0 0 1 1 0 1 0 0 0 2 0 0 5 6 0 0 0]
[0 1 5 0 1 1 0 0 5 6 6 6 6 1 2 4 0 6 0]
[0 0 1 0 0 0 0 0 0 1 0 0 0 4 0 0 4 0 0]
[0 0 0 1 5 2 0 0 4 5 2 1 2 5 4 0 1 6 0]
[0 0 0 0 1 3 0 5 0 0 2 2 4 0 0 0 4 0 1]
[0 0 0 0 0 2 0 1 4 3 4 1 2 5 4 0 5 0 0]
[0 0 0 0 0 1 0 6 0 0 6 1 6 4 0 1 6 0 5]
[0 0 0 0 0 4 0 3 0 4 3 0 3 3 4 3 3 0 3]
[0 0 0 0 0 0 2 0 0 1 4 0 0 0 6 0 0 2 0]
[0 0 0 0 0 1 5 5 0 2 2 6 1 3 5 3 1 1 3]
[0 0 0 0 0 4 0 2 6 4 6 1 2 3 3 2 1 2 5]
[0 0 0 0 0 3 0 3 0 6 3 4 0 3 4 4 3 2 0]
[0 0 0 0 0 2 0 2 3 0 4 3 3 2 1 2 0 1 2]
[0 0 0 0 0 3 2 0 5 0 4 3 0 1 0 4 5 0 6]
[0 0 0 0 0 6 0 0 0 2 4 4 6 5 0 2 2 0 2]
[0 0 0 0 0 0 0 4 0 0 0 0 0 5 0 0 0 0 3]
[0 0 0 0 0 6 0 0 0 1 0 4 0 1 3 4 2 4 0]
[0 0 0 0 0 5 0 3 0 2 6 0 2 1 5 6 4 0 6]
[0 0 0 0 0 1 6 6 6 3 5 2 0 4 2 5 2 2 1]

Regardons à plus grande échelle:

sage: M = random_matrix(GF(7), 200, sparse=True, density=1/10)
sage: len(M.nonzero_positions())
3806
sage: len(gauss(M, 50).nonzero_positions())
23497

Problème

Beaucoup de matrices apparaissant dans les problèmes pratiques sont structurées:

Matrices par bandes
Matrices companion
Matrices très creuses

L’algorithme de Gauß ne préserve pas ces structures!

Et pourtant:

sage: M = random_matrix(GF(7), 10000, sparse=True, density=3/10000)
sage: M.rank()
9263

Comment cela marche-t-il???

Algorithmes de type «boîtes noire»¶

On cherche des algorithmes dont la complexité soit contrôlée non seulement par la taille \(n\) de la matrice, mais aussi par son nombre \(m\) de coefficients non nuls.

Algorithme de Wiedemann¶

Problème

Calculer le polynôme minimal d’une matrice

Exercice

Soit \(P\) le polynôme minimal d’une matrice carrée \(M\).

Soient \(U\) et \(V\) deux vecteurs.

Montrer que la suite de nombre \(u_k = U M^k V\) satisfait une relation de récurence donnée par les coefficients de \(P\).

Solution

Todo

rédiger

Rappel: Algorithme de Berlekamp-Massey

L’algorithme de Berlekamp-Massey permet, étant donné une suite \(s_{1},\dots,s_{n}\) d’éléments d’un corps de trouver la plus petite relation de récurrence satisfaite par cette suite. Les coefficients de cette relation de récurrence sont traditionnellement encodés sous la forme d’un polynôme. Encore une conséquence d’Euclide étendu …

Voir TP pour les détails.

Algorithme de Wiedemann

Prendre des vecteurs \(U\) et \(V\) aléatoires
Déterminer les premiers termes de la suite \(u_k\) en calculant itérativement \(V, MV, M^2V, \ldots\)
En déduire par Berlekamp-Massey la relation de récurence minimale qu’elle satisfait
Cette relation divise le polynôme minimal \(P\) de \(M\)
Réitérer «suffisamment de fois»

Remarques

On n’a eu besoin de calculer que des produits \(MV\)
On voit \(M\) comme un endomorphisme
Complexité mémoire bornée par \(n\)

Application: calcul d’inverses¶

Exercice

Supposer que le polynôme minimal de \(M\) soit \(X^3-2X+1\).

Déterminer l’inverse de \(M\).

Application: calcul du rang¶

Voir TP.

Algorithme de Faddeev-Leverrier¶

http://en.wikipedia.org/wiki/Newton%27s_identities

Todo

Rédiger:

Étape 1: matrice triangulaire

Étape 2: sur un corps algébriquement clos, on triangularise

Étape 3: généralisation à un corps quelconque, avec extension implicite du corps is besoin

Rappeler les identités de Newton, avec démo Sage

Todo

Il reste 1/2h; soit attaquer le TP, soit prendre le temps ci-dessus

Travaux Pratiques¶

Todo

rajouter un exo sur Faddeev-Leverrier

Berlekamp Massé¶

Exercice: Berlekamp-Massey

L’algorithme de Berlekamp-Massey permet, étant donné une suite \(s_{1},\dots,s_{n}\) d’éléments d’un corps de trouver la plus petite relation de récurrence satisfaite par cette suite. Les coefficients de cette relation de récurrence sont traditionnellement encodés sous la forme d’un polynôme.

Cette algorithme est implanté dans Sage par la fonction berlekamp_masse(). Vous pouvez au choix faire quelques essais avec cette fonction et passer à l’exercice suivant ou …

Implanter l’algorithme de Berlekamp-Massey, soit en vous servant de [Massey.1969]: Shift-register synthesis and BCH Decoding James L. Massey, IEEE transactions on information theory, 1969, ou via l’algorithme d’Euclide étendu décrit dans le texte sur Wiedemann ou, avec plus de détails dans le texte sur le code de Goppa.

Proposition de correction.

Wiedemann¶

Exercice: Polynome minimal et Wiedemann sur un exemple

Prendre \(n=10\). Construire une matrice carrée \(M\) aléatoire de dimension \(n\) dont les valeurs propres sont dans \(\{0,1,2\}\) avec des multiplicités quelconques; on pourra soit le faire à la main, soit utiliser random_matrix() avec l’algorithme diagonalizable; on pourra tirer les multiplicités au hasard avec IntegerVectors.
Calculer son polynôme minimal avec la méthode minimal_polynomial.
Construire un vecteur aléatoire colonne \(v\) et un vecteur aléatoire ligne \(w\) de tailles \(n\). Calculer la suite \((w\times M^{k}\times v)_{k=0,\dots,2n}\).
Vérifier sur machine qu’elle suit une relation de récurence dont les coefficients sont donnés par le polynôme minimal de \(M\) (attention: les coefficients apparaissent dans l’ordre inverse de la convention utilisée dans [Massey.1969]). Le prouver.
Réciproquement, utiliser l’algorithme de Berlekamp-Massey pour retrouver le polynôme minimal de \(M\).

Exercice: Implantation de l’algorithme de Wiedemann

Écrire une procédure endomorphisme qui prend une matrice \(M\) en argument, et renvoie l’endomorphisme correspondant, c’est-à-dire la fonction qui à un vecteur \(v\) associe le vecteur \(M\times v\).
Finir d’implanter une procédure wiedemann(f, V) qui prend un endomorphisme \(f\) et l’espace sur lequel il agit, et calcule son polynôme minimal en utilisant l’algorithme de Wiedemann.
Vérifier le résultat sur la matrice précédente.
Écrire la fonction de multiplication par une matrice diagonale, la fonction de multiplication par une matrice tridiagonale. Utiliser Wiedemann pour calculer le polynôme minimal de quelques matrices de ce type.
Évaluer la complexité expérimentale de ces calculs. Comparer avec la méthode \(minpoly\) du système.

Exercice: Calcul du rang par préconditionnement par produit de matrices diagonales.

Fabriquer des matrices carrées raisonablement aléatoires de rang environ \(\frac{n}{2}\), dont les valeurs propres sont dans \(\{0,1,2\}\) (cf. l’exercice sur Wiedemann pour des indications).
Tester expérimentalement le théorème 2 page 7 de Computing the rank of large sparse matrices over finite fields Jean-Guillaume Dumas et Gilles Villard, Computer Algebra in Scientific Computing, 2002.

Une conjecture sur les matrices d’incidence arbres / forêts¶

On s’intéresse aux graphes simples (pas de boucles, pas d’arêtes multiples, pas d’orientation, …) à isomorphie près (les sommets ne portent pas d’étiquette permettant de les distinguer). Une forêt est un graphe acyclique; un arbre est une forêt connexe.

Exercice

Fabriquer la liste de toutes les forêts à \(6\) sommets et \(4\) arêtes, à isomorphie près. Que constatez-vous?

Indication: essayer:

sage: for g in graphs(5): show(g)

puis utiliser les options property et size et la méthode is_forest.

Fixons un entier \(n\). On va considérer la matrice \(T_n\) dont

Les colonnes sont indexées par les arbres à \(n\) sommets (et donc \(n-1\) arêtes);
Les lignes sont indexées par les forêts à \(n\) sommets et \(n-2\) arêtes;
Le coefficient \(c_{f,t}\) compte le nombre d’arêtes de \(t\) telles que si l’on supprime cette arête on obtient un graphe isomorphe à \(f\).

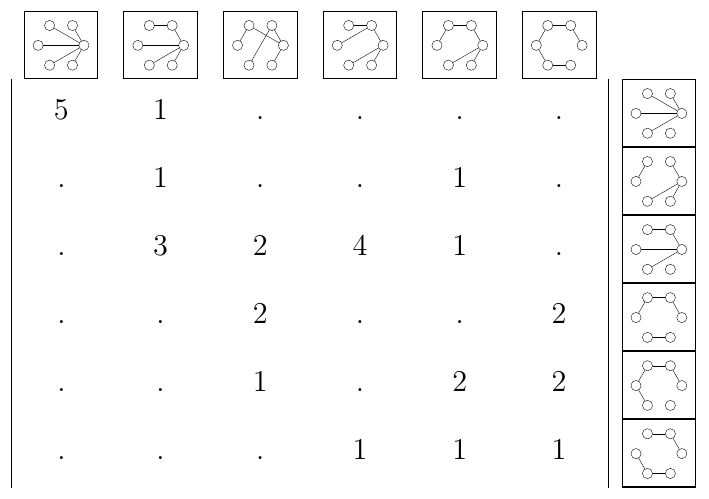
La matrice d'incidence `T_6` des graphes acycliques à `6` sommets et `5` arêtes versus ceux à `4` arêtes

Exercice

Écrire une fonction qui construit la matrice \(T_n\).

Indications:

Construire les deux listes de graphes

Par défaut, les graphes sont mutables, et on ne peut pas les mettre dans un dictionnaire:

sage: G = Graph([[1,2]])
sage: {G: 1}
Traceback (most recent call last)
...
TypeError: graphs are mutable, and thus not hashable

Pour corriger cela, il faut rendre le graphe immutable:

sage: G = G.copy(immutable=True)
Graph on 2 vertices
sage: {G: 1}
{Graph on 2 vertices: 1}

Numéroter les graphes dans les deux listes en utilisant sage.combinat.ranker.from_list().
Utiliser les méthodes copy et delete_edge pour obtenir \(f\) par suppression d’une arête de \(t\). Puis utiliser la méthode canonical_label pour mettre \(f\) sous forme canonique à isomorphie près.

Exercice

Explorer les propriétés de la matrice \(T_n\).

Pour les curieux, voir arXiv:0912.2619, p. 21.

Option Algèbre et Calcul Formel de l’Agrégation de Mathématiques: Algèbre linéaire rapide¶

Méthodes modulaires et généralisations¶

Introduction¶

Analyse: Complexité arithmétique versus complexité en bits¶

Méthodes modulaires et multimodulaires¶

Exemple: le calcul du déterminant¶

Exemple: bornes sur le rang¶

Généralisations¶

Variante: méthodes \(p\)-adiques¶

Expansion \(p\)-adique¶

Algorithmes de type «Boîte noire»¶

Problème¶

Algorithmes de type «boîtes noire»¶

Algorithme de Wiedemann¶

Application: calcul d’inverses¶

Application: calcul du rang¶

Algorithme de Faddeev-Leverrier¶

Travaux Pratiques¶

Berlekamp Massé¶

Wiedemann¶

Une conjecture sur les matrices d’incidence arbres / forêts¶

This Page

Table of Contents

Previous topic

Next topic